Deep Learning Summary
Contents
Part I Machine Learning
1 The Task
Machine learning allow us to tackle tasks that are too difficult to solve with fixed programs written and designed by human beings. Machine learning is interesting because developing our understanding of machine learning entails developing our understanding of the principle that underlie intelligence.
Learning is our means of attaining the ability to perform the task.
The most important task in Machine Learning are:
-
Classification: The computer program is asked to specify which of k categories some inputs belongs to. The learning algorithm is asked to produce a function . An example of classification is object recognition. To perform classification the error function is usually the cross entropy.
-
Binary classification: It is enough to use one output neuron with a or function. The two classes are the extreme points of the function.
-
Multinomial classification: we have to decide to which class belongs the input: . It’s not good to use one output neuron with linear output for this task because it’s like saying that there are precedences between classes. It’s possible to use 1-out-of-m encoding. There are m output neurons, one for each class, with function.
-
-
Regression: The computer program is asked to predict a numerical value given some input. The learning algorithm is asked to output a function . In the regression case it’s not possible to use a or function because they are bounded between and [-1,+1] respectively. There is the need to have a function that covers all possible values. There is the possibility to use a linear function (RELU, Rectified Linear Unit). If the range of output is limited we can normalize it and use function.
2 Perceptrons
2.1 Activation Function
The activation function of a neuron depends on its activation value:
In this activation value it’s taken into account also the bias. The bias is with value -1 and the corresponding weight is .
The most common used activation function are:
-
Sigmoid Function: continuous approximation of a step function.
This is between 0 and 1.
-
Hyperbolic Tangent: continuous approximation of a sign function.
-
Linear Function: the unit with linear function is called also Relu (Rectified Linear Unit).
-
Sign Function: the usual sign function.
2.2 Representational Power of Perceptrons
We can view perceptron as representing hyperplane decision surface in the n-dimensional space of instances (points). The perceptron outputs 1 for instances lying on one side of the hyperplane and -1 for instances lying on the other side. The equation for this decision hyperplane is . Some sets of positive and negative examples cannot be separated by any hyperplane. Those that can be separated are called linearly separable sets.
Perceptron can represent all the primitive boolean function AND, OR, NAND and NOR. Some boolean functions cannot be represented by a single perceptron, such as XOR function. Ability of perceptron to represent the primitive function is important because every boolean function can be represented by some network of interconnected units based on them.
2.3 Hebbian Learning
The strength of a synapses increases according to the simultaneous activation of the relative input and the desired target.
In this way the next neuron learns that when the previous neuron fires, it has to fire. This is modeled with the increased strength of a synapse.
The weight change according to a delta function.
The weight’s change is applied only when the output doesn’t correspond to the target. Formally there should be () instead of t.
The delta function depends on:
-
: learning rate. The role of () is to moderate the degree to which weights are changed at each step.
-
t: target value.
-
: Input value of i-th input.
The product between the target and the i-th input selects the direction in which the weight should go. If they are both positive this means that there is a direct dependence between them, so the weight must increase.
This learning procedure can be proven to converge within a finite number of applications of the perceptron training rule to a weight vector that correctly classified all training examples, provided the training example are linearly separable and provided sufficiently small is used.
Hebbian Learning is not suited for multilayer perceptron. It’s difficult to know the input of hidden layers and the expected output of them because we do not know it.
3 Multi-Layer NN
3.1 Universal Approximation Theorem
The universal approximation theorem states that a feed forward neural network with a single hidden layer containing a finite number of neurons can approximate continuous function (also non linear) on compact subsets of with any desired non-zero error. The only assumption is that the activation function must be s-shaped.
It is not the specific choice of the activation function, but rather the multilayer feedforward architecture itself which gives neural networks the potential of being universal approximators. The output units are always assumed to be linear.
The UAT (Universal Approximation Theorem) means that reagrdless of what function we are trying to learn, we know that a large multi-layer FFNN will be able to represent this function. However we are not guaranteed that the training algorithm will be able to learn that function.
Training algorithm can fail for two reasons:
-
The optimization algorithm used for training may be not able to find the value of parameters that correspond to the desired function.
-
The training algorithm might choose the wrong function due to overfitting.
The no free lunch theorem shows that there no universally superior machine learning algorithm.
In summary, a feedforward network with a single layer is sufficient to represent any function, but the layer may be infeasibly large and may fail to learn and generalize correctly. In many circumstances, using deeper models can reduce the number of units required to represent the desired function and can reduce the amount of generalization error.
3.2 Gradient Descent and the Delta Rule
The perceptron rule fails to converge if the examples are not linearly separable.
The delta rule instead converges toward a best-fit approximation to the target concept.
The key idea is to use gradient descent to search the hypothesis space of possible weight vectors to find weights that best fit the training examples. This rule is important because gradient descent can serve as the basis for the backpropagation algorithm.
Learning can be summarized in this way:
Where
So we move in the opposite direction wrt the gradient of the Error function wrt the weight. In this way we try to search a local minima.
To overcome the problem of local optima we can restart the problem multiple time.
3.3 Differentiable Unit
Which type of activation function should we use in a multilayer NN?
Multiple layers of cascaded linear units still produce only linear functions and we prefer networks capable of representing highly non-linear functions. What we need is a unit whose output in a non linear function of inputs but whose output is also a differentiable function of its input. One solution is the sigmoid unit, based on a smoothed, differentiable threshold function.
3.4 Backpropagation Algorithm
The backpropagation algorithm learns the weights for a multilayer network, given a network with a fixed set of units and interconnections. It employs gradient descent to attempt to minimize the squared error between the network output values and the target values for these outputs.
The goal is to approximate a target function t given a set of N observations.
We want to minimize the error E:
Where is the output of the net given the n-th example.
Output Weights
Compute the derivative of E wrt an output weight :
The derivative of wrt is zero because it doesn’t depend on the weight.
Notice that is computed this way:
Where is the activation function of the j-th hidden unit.
So there is only one element of y that depends on , :
In this way we are approximating the function with the tangent hyperplane.
Notice that this computation regards all the examples.
The derivative of the error with respect to an output weight is the derivative of the error function multiplied by the derivative of the activation function of the output unit and by the activation function of the relative hidden unit (all with minus sign).
If we have more than one output unit we have to sum all the gradients with respect to each unit.
Hidden Weights
We have to compute the derivative of the error wrt .
Following the above approach:
3.4.1 Chain Rule
It’s easy to see that there is a pattern under the previous equations and this is the chain rule:
And the same it’s for input neurons.
3.4.2 Hebbian vs Backpropagation
Hebbian rule takes 1 sample and changes weights. Every sample will change weights. This is called Online Learning.
In Backpropagation in 1 step we minimize the error on all the training data. This is called Batch Learning.
There is a trade off between online and batch, when we cannot load all the dataset: MiniBatch. Divide dataset in sets, load them, compute the gradient and apply it.
4 Maximum Likelihood Estimation
We would like to have some principle from which we can derive specific functions that are good estimators for different models.
The most common principle is the maximum likelihood principle.
Consider a set of m examples drawn independently from the true but unknown data generating distribution . Unknown is in term of parameters.
Let be a parametric family of probability distributions over the same space indexed by . In our cases is the set of weights. We have a distribution that depends on weights in an unknown way. We want to estimate the set of weights for maximizing the truth of the distribution.
The max likelihood estimator for is:
| (1) |
Since the data are iid, we can use the product of all probability. This can cause numerical instability and underflow.
Apply the logarithm that does not change the index of the max:
| (2) |
Mean Squared Error (MSE) is the cross entropy between the empirical distribution and a Gaussian Model.
We can see MLE (Maximum Likelihood Estimation) as an attempt to make the model distribution match the empirical distribution from data.
Bayes Theorem
In Machine Learning we are often interested in determining the best hypothesis from some space H, given the observed data D. We demand the most probable hypothesis given the data plus any initial knowledge about the prior probabilities of the various hypothesis in H. Bayes theorem provides a way to calculate the probability of an hypothesis based on its prior probability, the probability of observing various data given the hypothesis and the observed data itself.
is the prior probability of h and reflect any background knowledge we have about the chance that h is a correct hypothesis. It is the probability that h holds before seeing the training data.
If we do not have a prior knowledge we assign the same probability to each candidate.
denotes the prior probability that training data D will be observed.
In Machine Learning we are interested in the probability that h holds given the observed data. This is called posterior probability of . The posterior probability reflect the influence of the training data , in contrast to the prior probability which is independent of D.
| (3) |
As one might intuitively expect, increases with and with according to Bayes theorem. It is also reasonable to see that decreases as increases, because the more probable it is that D will be observed independent of h, the less evidence D provides in support of h.
In Machine Learning the learner considers some set of candidate hypothesis H and is interested in finding the most probable hypothesis h given the observed data D. Any such maximally hypothesis is called a maximum a posteriori (MAP).
Notice that we can remove P(D) because it’s independent from h.
If we assume every hypothesis is equally probable we obtain the likelihood estimation: . This is called maximum likelihood hypothesis:
4.1 ML and LSE
Is the least square error function a good error function for classification?
The goal is to approximate a target function given a finite set of observation N.
We assume the target function being affected by a white noise, otherwise it’s possible to approximate it by simply passing through all samples.
We assume the mean of the target function being the output of the net because in the ML approach the hypothesis is assumed to be true:
We have to learn w in such a way to maximize the probability .
Learning as estimating parameters of distribution . The strange thing here is that the mean is a function that depends on the current value.
Applying likelihood and loglikehood the result is that the least square error is a good choice for error function for the Noise Model and regression problems.
In case of classification problems the result is that the cross entropy function is good error function.
After having modeled the target function as a Bernulli:
5 Regularization
A central problem in machine learning is how to make algorithm that perform well not just on training data but also on new data (test set). Many strategies are used to explicitly reduce test error, possibly at the expense of increased training error. In this way we avoid overfitting and we improve generalization property of the net.
You don’t want to learn the noise but only the model.
Generalization is producing good result on new data never seen before.
Overfitting is when the model has learned well on training data but not very well on new data. It has memorized the training and it’s noise.
How to measure overfitting?
1. Hide data (test set) before learning
2. Train model and evaluate it on test set.
5.1 Early Stopping
When training large models with sufficient representational capacity to overfit the task, we observe that training error decreases steadily over time but validation set error begins to rise again.
When validation error increases this means we are loss generalization and we begin to overfit.
At this point is convenient to stop training and maintain the parameter setting at the point in time with the lowest validation set error. We run the algorithm for learning until the error on the validation set has not improved for some amount of time.
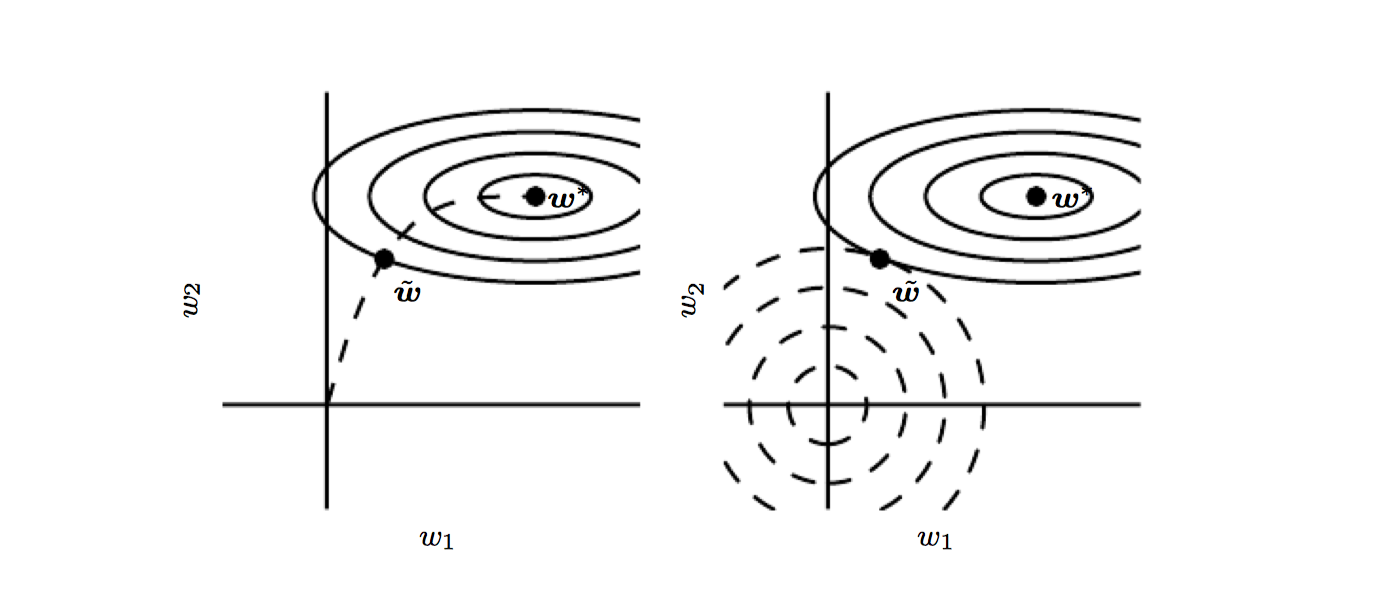
Early stopping is usually a good method to find out how many neurons we need in the hidden layer: compare different topologies wrt the validation error.
In the first phase of the training minimizing error is minimizing validation error. The network is learning common phenomenon between training and test.
In the second phase the net is learning something not related to the model. It is learning the noise inside the model and reducing its capability of generalization.
Cross Validation: Algorithm might be sensitive with respect to the split. It is possible to have 5 sets. Using 1 set for validation and the other for training. Train different model and take them all averaging the result.
Problem is when you do not have enough data, because you can’t split.
5.2 Weight Decay
The technique of regularization encourages smoother network mappings by adding a penalty term to the error function to give:
Here E is one of the standard error functions and the parameter controls the extent to which the penalty term influences the form of the solution. Training is performed by minimizing the total error function. The resulting error mapping is a compromise between fitting the data and minimizing .
In weight decay:
We know that to produce an over-fitted mapping with regions of large curvature requires relatively large values for weights. For small values the function is approximately linear. By using this type of regularizer the weights are encouraged to be small.
Let’s study the behavior of weights in time:
Supposing the term E is absent.
By solving this equation the function of weights in time is given by:
and so all weights decay exponentially to zero.
Bayesian Justification
The weight decay approach has also a Bayesian justification.
We know we want the weights being small. So we can suppose weights are:
Using Bayes’ formula:
and we want to find the weights that maximize this probability.
We obtain the following result:
Where M is the set of weights.
In this way we are penalizing network complexity introducing a bias. Weight decay is a way to constrain the network and decrease it’s complexity by keeping weights small.
How to find the best ?
Using cross validation with different values.
The more you increase the more you are penalizing large weights and improving generalization capabilities.
5.3 Bagging
Bagging (bootstrap aggregation) is a technique for reducing generalization error by combining several models.
Idea: train several models separately, then have all of the models vote on the output for test examples. Strategy of model averaging. Techniques ensemble methods.
Reason is that different models will usually not make the same errors on the test set.
- Create k different independent set by sampling from the original dataset. The datasets will have some shared examples and some unique examples. This helps in having independent errors.
- Train different models
- Average all models
Result: on average the result of averaged model will be better than any of those.
Begging is this: average independent classifier.
With independent errors the resulting error of the averaged model is less than any of its member. If the error are perfectly correlated the resulting error remains the same.
Let’s suppose errors are a multivariate Gaussian with 0 mean, v variance and c covariance.
The expected squared error of the ensemble is:
So, if the error are uncorrelated () the expected squared error is , so it decreases linearly with the numbers of models. If the errors are perfectly correlated () and the expected error is only v (remains the same).
This underlie the importance of having independent errors and so the importance of having different datasets.
5.4 Dropout
Dropout provides a computationally inexpensive but powerful method of regularizing a broad family of models.
Dropout can be thought of as a method of making bagging practical for ensembles of very many large neural networks. Bagging involves training multiple models and evaluating them on each test examples. This is impractical when NN are large. Dropout provides an inexpensive approximation to training and evaluating a bagged ensemble of exponentially many neural network.
Dropout trains the ensemble consisting of all subnetworks that can be formed by removing non-output units from an underlying base network.
The term dropout refers to dropping out units (hidden and visible) in a neural network. By dropping out a unit, we mean temporarily removing it from the network, along with all its incoming and outgoing connections. Applying dropout to a network is like sampling a thinned network from it. A NN with n units can be seen as a collection of possible thinned NNs. These networks all share weights so that the total number of parameters is still the same of one NN.
For each presentation of each training case, a new thinned network is sampled and trained. So training a NN with dropout can be seen as training a collection of thinned NNs with extensive weight sharing, where each thinned network gets trained very rarely.
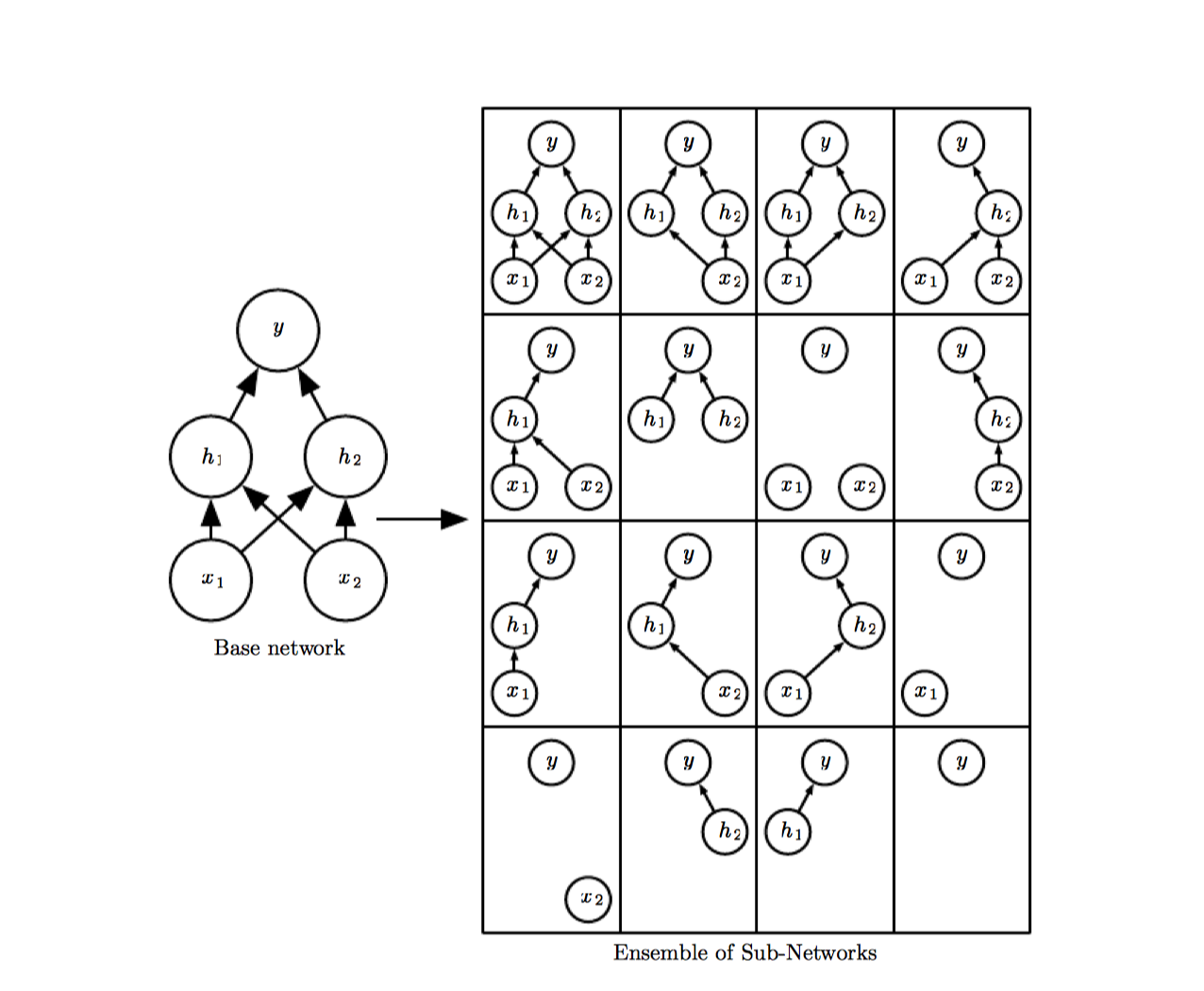
At test time is used a single NN without dropout. The weights of this NN are a scaled-down version of the trained weights. If a input unit is retained with probability p at test time, the outgoing weights of that unit are multiplied by p at test time. By doing this scaling, networks can be combined into a single NN to be used at test time.
Part II Deep Learning
Fast visual recognition in the mammalian cortex seems to be a hierarchical process by which the representation of the visual world is transformed in multiple stages from low-level retinotopic features to high-level, global and invariant features, and to object categories. Every single step in this hierarchy seems to be subject to learning. In the previous concept of multilayer feed forward NN the net doesn’t learn in every step. The previous architecture was made of a hand-crafted feature extractor that converts the raw data in a convenient representation for the net. This feature extractor it’s not trainable, since it was “hard-coded”.
How does the visual cortex learn such hierarchical representations by just looking at the world? How could computers learn such representations from data?
In deep learning framework the net learns also a convenient representation for data, the idea of feature learning.
Deep learning assumes it is possible to learn a hierarchy of descriptors with increasing abstraction, layers are trainable feature transforms.
In image recognition:
• Pixel → edge → texton → motif → part → object
In DL there isn’t the fear of overfitting because we have a huge amount of data.


6 Convolutional Networks
Data from natural sensors often come to us as a multi-dimensional arrays in which local group of values are correlated, and the local statistics are invariant to the particular location in the array.
Convolutional Neural Networks are a specialized kind of NN for processing data with a grid-like topology, used mostly for Image Analysis and NLP.
Convolutional networks are NN that use convolution in place of a general matrix multiplication in at least one of their layers.
Convolution (for image processing) is a summation of the products between original pixels and the kernel (mask, convolutional filter).
In short it’s the implementation of a digital filter.
The statistics of images are translation invariant, which means that if one particular filter is useful on one part of an image, it is probably useful on other parts of the image as well. Multi Layer perceptron have little invariance to shifting, scaling and other form of distortion.
The filter bank in each stage is a bank of convolution kernels applied to slices of the input. A filter bank is an array of kernels that extract different feature of the image. There can be one kernel extracting edges, another extracting a different feature. The CNN learns values of filters on its own during the training process.
It’s important to notice that convolution captures local dependencies in the input.
The pooling layers are subsampled spatially, which reduces the spatial resolution of the representation and makes the representation vary smoothly with translations and small distortions of the input.
6.1 Convolution Operation
Convolution is an operation on two functions of a real valued argument.
| (4) |
In CNN the first argument (the function x) is the input while the second argument (the function w) is the kernel. The output is the feature map.
If we transfer the idea from a continuos dominion to a discrete dominion we obtain the 5.
| (5) |
The input is usually a multidimensional array of data and the kernel is usually a multidimensional array of parameters adapted by the learning algorithm.
Notice that the learning algorithm will learn the appropriate values of the kernel in the appropriate place.
Since the input image is a matrix, the convolution operation is 2D:
| (6) |
Notice how the convolution depends on two parameters i,j.
I,J are the dimensions of the input image, while M,N are dimensions of the Kernel.
Commutative property of convolution arises because we’ve flipped the Kernel relative to the input, but there is not this need in Machine Learning. So we do convolution without kernel flipping:
| (7) |
The convolution layer performs the following:
-
A Kernel slides over input feature map.
-
At each kernel position, element-wise product is computed between the kernel and the overlapped input set.
-
Result is summed up and constitute the output feature map.
6.2 Architecture
In a CNN each layer has a depth, in the sense that multiple filters are applied to the same image.
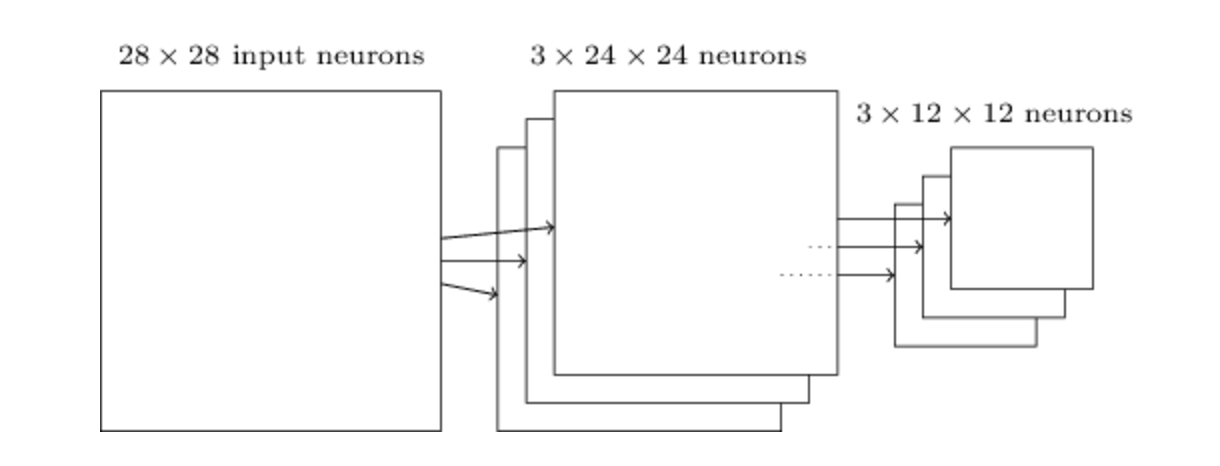
Each filter is responsible for extracting a particular feature of the input.
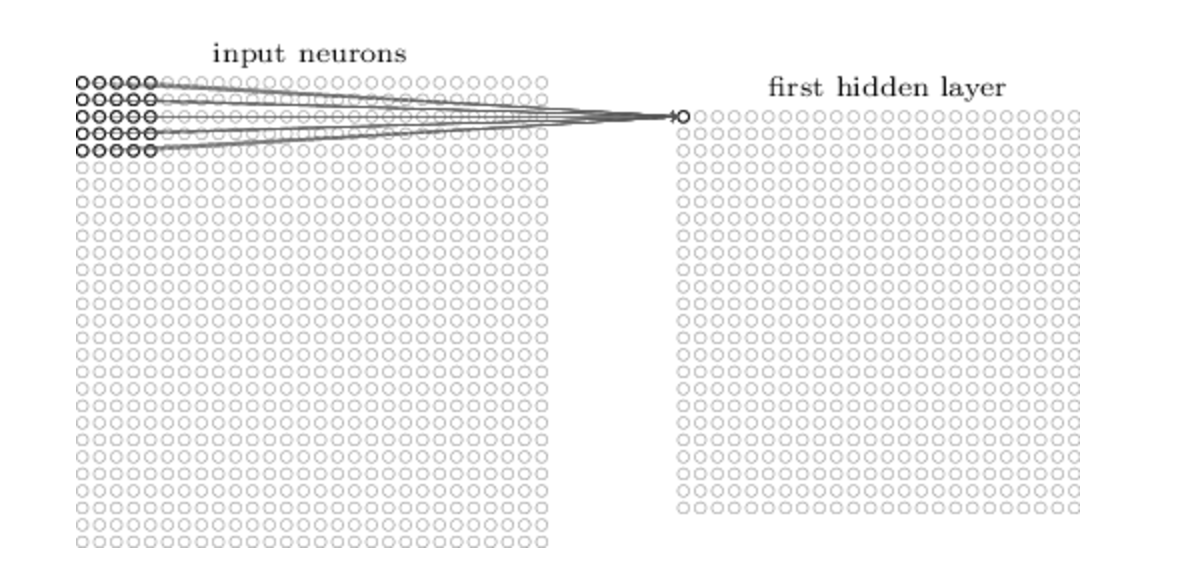
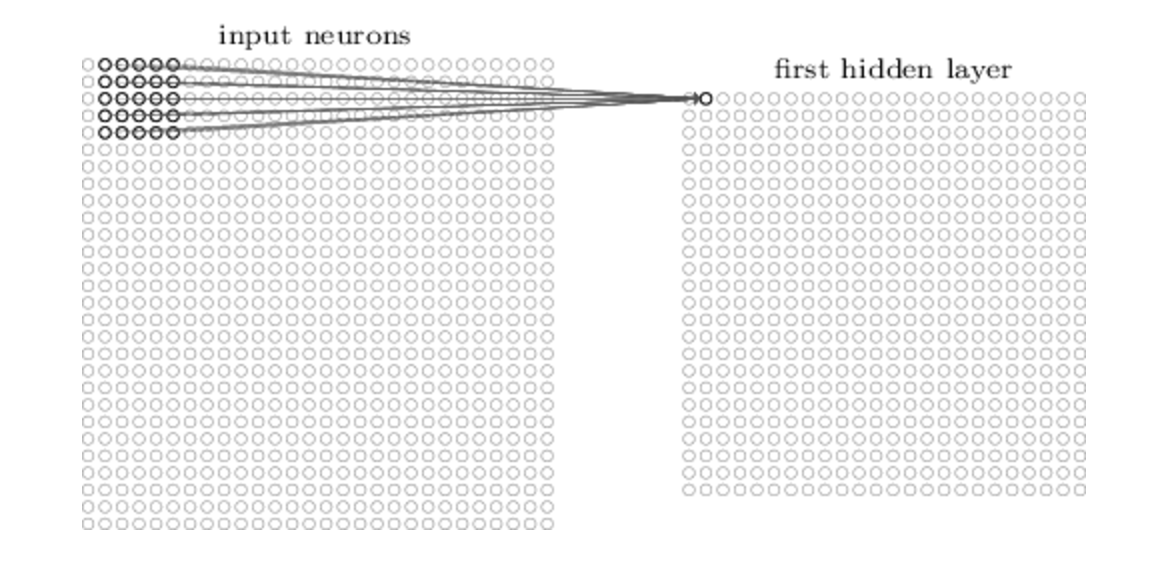
Each neuron in the hidden layer is connected to a small region of the input neuron, its receptive field. For each local receptive field there is an hidden neuron in the first hidden layer.
It’s important to notice that, even if there are multiple hidden neurons, the weights are shared across all neurons. In this way neurons extract the same features.
6.3 Characteristics
Convolution is fundamental for three concepts that can improve a machine learning system.
Sparse Interactions
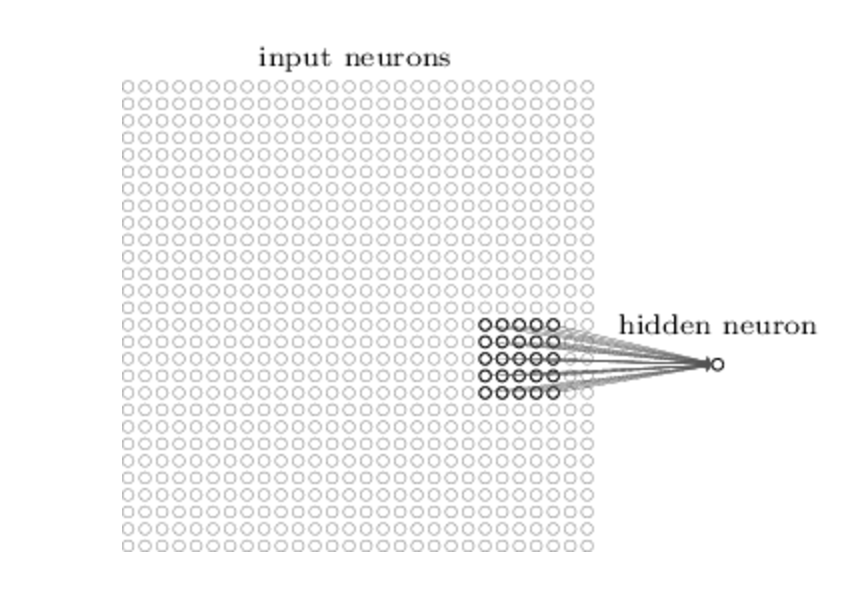
In traditional NN every output unit interacts with every input. This means a lot of parameters and sensitivity to input changes.
CNN have a sparse interaction due to the fact that the kernel is smaller than the input. We need to store fewer parameters, which both reduces the memory requirements of the model and improves its statistical efficiency.
Each neuron is connected only with its receptive field and it’s not affected by other input.
Parameter Sharing
This term refers to using the same parameter for more than one function in a model. In CNN each member of the kernel is used at every position of the input. Parameter sharing means that rather than learning a separate set of parameters for every location, we learn only one set share across all input. This reduce the storage requirements of the model.
The same weights are shared among all neurons, in this way all neurons detect the same feature. The same weights is used for the same position in all the neurons.
The training algorithm is similar to the training algorithm of Elman NN.
Equivariant Representations
In the case of convolution parameter sharing causes equivariance to translation.
Equivariant function: when the input changes the output changes in the same way. Imagine a function shifts every pixel of an image one unit to the right. If we apply that function and then convolution, the result will be the same as if we apply convolution and then the function. This is useful for when we know that some function of a small number of neighboring pixel is useful when applied to multiple input location. The same edges appear more or less everywhere in the image so it’s practical to share parameters across the entire image.
6.4 Pooling
A pooling function replaces the output of the net at a certain location with a summary statistics of the nearby outputs. Example of pooling function are max-pooling or average.
Pooling helps to make the representation become approximately invariant to small translations of the input. Invariance to local translation can be a very useful property if we care more about the existence of a property (feature) instead of the exact position of it. Because pooling summarizes the response over a whole neighborhood, it is possible to use fewer pooling units than detector units.
Pooling over spatial regions produces invariance to translation, but if we pool over the outputs of separately parametrized convolutions, the features can learn which transformations to become invariant to.
Pooling progressively reduces the spatial size of the image and helps to obtain invariance wrt rotation, scaling and other transformation.
7 Autoencoders
Unsupervised algorithms are important for deep learning. The basic procedure is to pre-train each stage of a network in an unsupervised manner one after the other. After all stages of a network have been pre-trained, the entire network is fine-tuned using supervised learning.
Advantages:
-
Unsupervised pre-training place the system in a favorable starting point for supervised fine-tuning that will produce better performance results.
-
Unsupervised leaning leverages the availability of massive amount of unlabeled data.
An autoencoder is a neural network that is trained to copy its input to its output. It has an hidden layer h that describes a code used to represent the input.
Encoder function .
Decoder function .
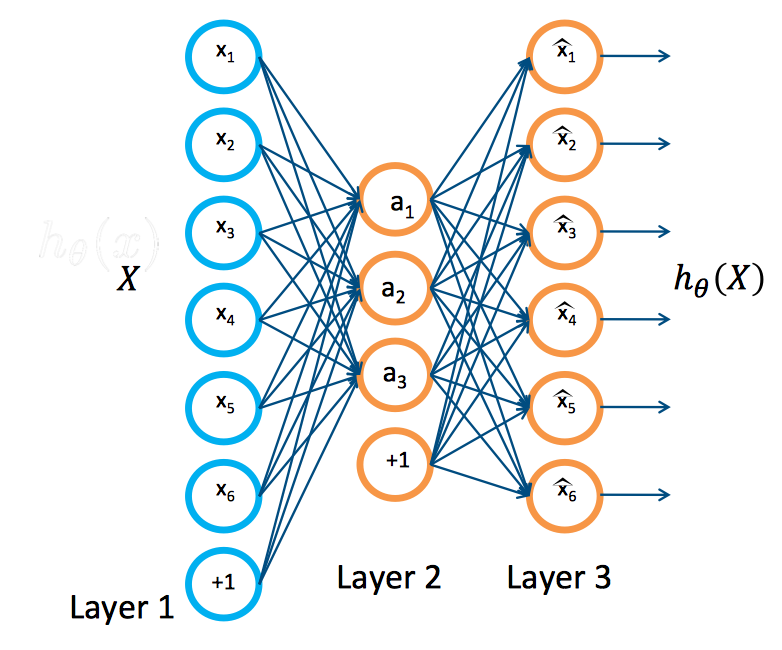
Autoencoders are designed to be unable to learn to copy perfectly. Because the model is forced to prioritize which aspects of the input should be copied, it often learns useful property of the data.
Autoencoders were used for dimensionality reduction or feature learning.
Copying the input to the output may sound useless, but we are typically not interested in the output of the decoder. Instead we hope that training the autoencoder to perform the input copying task will result in h taking on useful property.
One way to obtain useful feature is to constrain h to have smaller dimension than x. In this case autoencoder is called under-complete. Learning an under-complete representation forces the autoencoders to capture the most salient features of the training data.
Training a sparse autoencoder from a dataset can be done with
| (8) |
Where the first term is the error due to reconstruction and the second term is an L1 sparsity term. The term is the term referred to the code layer.
In this way we penalize the use of parameters and we force the network to be sparse.
Sparse autoencoders are typically used to learn features for another task such as classification. An autoencoder that has been regularized to be sparse must respond to unique statistical features of the dataset it has been trained on. In this way training to perform a copy task with sparsity penalty can yield a model that has learned useful property as a byproduct.
Unlike other regularizers such as weight decay, there is not a straightforward Bayesian interpretation to this regularizer.
After having trained a sparse autoencoder it is possible to throw away the decoder layer and use the encoder layer as input for another autoencoder.
At the end we have a new representation for the input and it’s possible to use it to feed a supervised learning algorithm.
The autoencoder tries to learn a function x. In other words, it is trying to learn an approximation to the identity function, so as to output x̂ that is similar to x. The identity function seems a particularly trivial function to be trying to learn; but by placing constraints on the network, such as by limiting the number of hidden units, we can discover interesting structure about the data. As a concrete example, suppose the inputs x are the pixel intensity values from a 10×10 image (100 pixels) so n=100, and there are =50 hidden units in layer L2. Note that we also have y. Since there are only 50 hidden units, the network is forced to learn a ”compressed” representation of the input. I.e., given only the vector of hidden unit activations a(2), it must try to ”reconstruct” the 100-pixel input x. If the input were completely random—say, each comes from an IID Gaussian independent of the other features—then this compression task would be very difficult. But if there is structure in the data, for example, if some of the input features are correlated, then this algorithm will be able to discover some of those correlations.
8 Time series Analysis
RNN are used for time series analysis. RNN are a family of NN used for processing sequential data.
The task is to predict the next value y(t+1) given the current input x(t) and all the previous x(t-1).
There are three way to do prediction:
-
Standard Feedforward: we can do regression from x(t) to y(t+1) but we cannot capture earlier dependencies
-
FF with delayed input: we can keep a windows of k inputs and apply regression from x(t-k) … x(t) to y(t+1). The problem is that we do not know k.
-
Recurrent Neural Network: we can add a new unit b to the hidden layer and a new input unit c(t) to represent the value of b at time (t − 1). b thus can summarize information from earlier values of x arbitrarily distant in time.
8.1 Elman
Elman network is a NN with some context units. Context units are used to memorize the previous activations of the hidden units and can be considered to function as one-step time delays.
At a specific time k, the previous activations of the hidden units at time k-1 and the current input at time k are used as inputs to the network. Theoretically an Elman network is able to model a nth-order dynamic system.
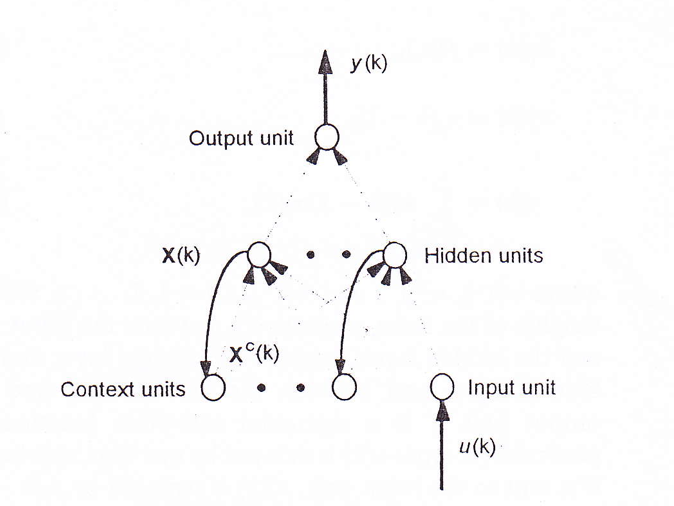
To train this net is possible to use the backpropagation through time (BTT). This is a simple algorithm based on network unfolding:
-
Perform network unfolding (using U unwrapping steps) and obtain a NN with weights depending on time. Notice that the same weight must have the same value over time.
-
Train the network like a simple feed forward NN:
-
Update all the weights with the formula above. In this way the weights are constrained to be the same over time.
We need to specify the initial activity state of all hidden units: we can treat the initial states as parameters to be learned.
Vanishing Gradient Problem
It turns out that training the RNN causes the gradient either vanishing or exploding.
Since activation function is sigmoidal is between 0 and 1, so going back in the past the gradient vanishes. After a few unroll there’s no information arriving to weights.
8.2 Lstm
Recurrent Neural Network are Neural Network with cell with recurrent arcs. In practice the output of some cells depends on the previous output, in this way NN can perform sequence prediction.
In a RNN the hidden state is:
In this way the current state depends both on the previous state end on the current input.
In this way the output of the net depends on the current state but since it depends on the previous state it can learn sequences. The important thing here is that the self recurrent weight does not depend on time, so it’s shared among all periods.
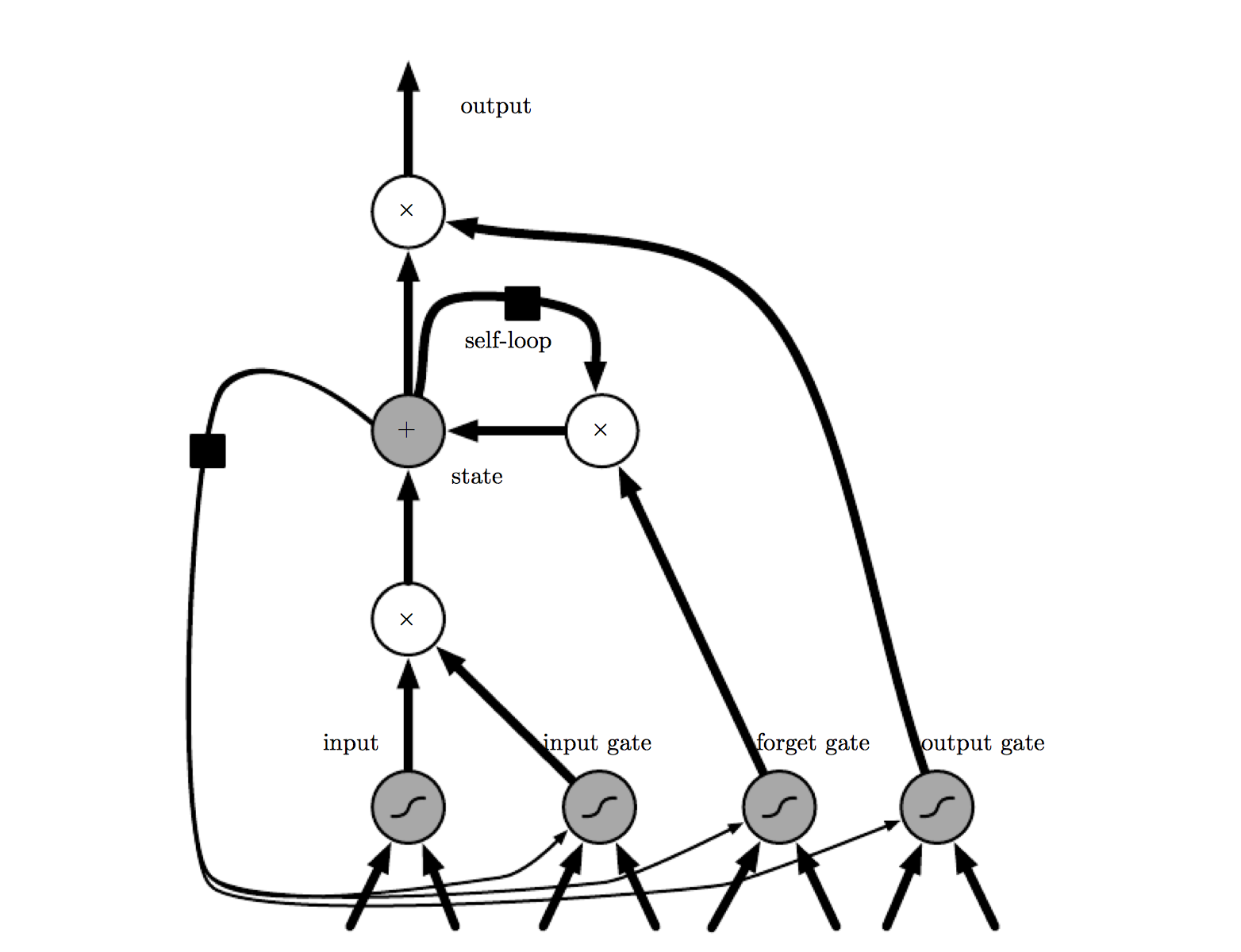
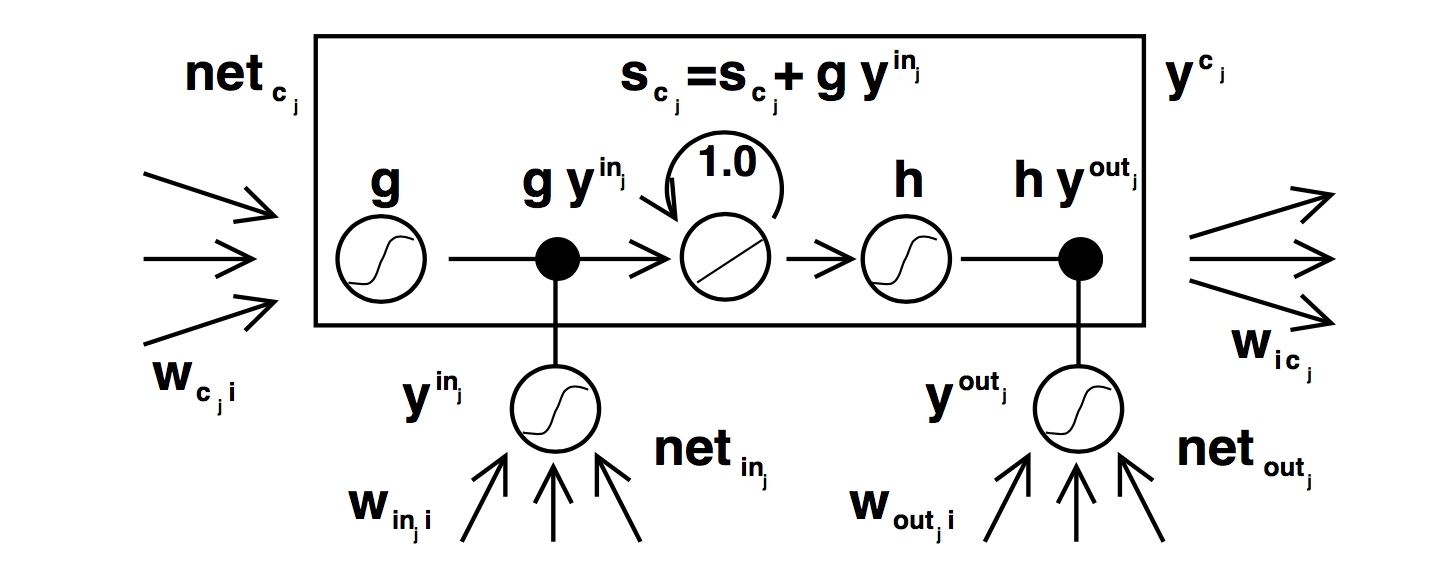
Like leaky units, gated RNNs are based on the idea of creating paths through time that have derivatives that neither vanish nor explode.
Leaky units did this with connection weights that were either manually chosen constants or were parameters. Gated RNNs generalize this to connection weights that may change at each time step.
Leaky units allow the network to accumulate information (such as evidence for a particular feature or category) over a long duration. However, once that information has been used, it might be useful for the neural network to forget the old state. For example, if a sequence is made of sub-sequences and we want a leaky unit to accumulate evidence inside each sub subsequence, we need a mechanism to forget the old state by setting it to zero. Instead of manually deciding when to clear the state, we want the neural network to learn to decide when to do it. This is what gated RNNs do.
We know that Elman RNN suffers of vanishing or exploding gradient. LSTM is a new architecture for RNN enforcing constant error flow through internal states of special units.
To enforce constant error flow:
This can be achieved by using identity function for and by setting the weight equals to 1.
The gate unit have been introduced in order to overcome the problem of weight conflict.
Input weight conflict
Consider a unique weight from the unit i to the memory cell j. This weights has to be used for both storing certain inputs and ignoring others. Given that the weight will receive conflicting weight updates during time making learning difficult.
Output weight conflict
Consider a unique weight from memory cell j to another cell k. This weight must be used for both retrieving information from the memory cell and for preventing k from being disturbed from j.
This causes weight update conflict.
Gate Units
Gate units are used to avoid weight conflict.
A multiplicative input gate unit is introduced to protect the memory content stored from perturbation by irrelevant inputs. A multiplicative output gate unit is introduced is introduced to protect other units from perturbation by currently irrelevant contents stored. The resulting is a memory cell. Each memory is built around a central linear unit with a fixed self connection.
For instance, an input gate (output gate) may use inputs from other memory cells to decide whether to store (access) certain information in its memory cell.
-
INPUT GATE: Information gets into the cell whenever its “write” gate is on.
-
FORGET GATE: The information stays in the cell so long as its “keep” gate is on.
-
OUTPUT GATE: Information can be read from the cell by turning on its “read” gate.
To ensure non-decaying error backprop through internal states of memory cells, errors arriving at memory cell net inputs (for cell , this includes , , ) do not get propagated back further in time (although they do serve to change the incoming weights). Only within 2 memory cells, errors are propagated back through previous internal states . To visualize this: once an error signal arrives at a memory cell output, it gets scaled by output gate activation and h’. Then it is within the memory cell’s CEC, where it can ow back indefinitely without ever being scaled. Only when it leaves the memory cell through the input gate and g, it is scaled once more by input gate activation and g’ . It then serves to change the incoming weights before it is truncated.