Most of the problems tackled by Reinforcement Learning are typically modeled as Markov Decision Processes in which the environment is considered a fixed entity and cannot be controlled. Nevertheless, there exist several real-world examples in which a partial control on the environment can be exercised by the agent itself or by an external supervisor. For instance, in a car race the driver can set up his/her vehicle to better suit his/her needs. With the phrase environment configuration we refer to the activity of altering some environmental parameters to improve the performance of the agent’s policy. This scenario has been recently formalized as a Configurable Markov Decision Process (CMDP) (Metelli et al., 2018). Formula One engineers have to configure their cars (e.g. wings, tyres, engine, brakes) to minimize lap time. In industry, machines have to be configured to maximize the production rate. These are cases in which the goal of the configuration is to improve performance, however in the case of car race it is possible for the supervisor to improve the learning speed of the pilot by presenting tracks of different difficulty.


In our paper “Reinforcement Learning in Continuous Configurable Environments”, accepted at ICML 2019, we propose a trust-region method, Relative Entropy Model Policy Search (REMPS), able to learn both the policy and the MDP configuration in continuous domains without requiring the knowledge of the true model of the environment.
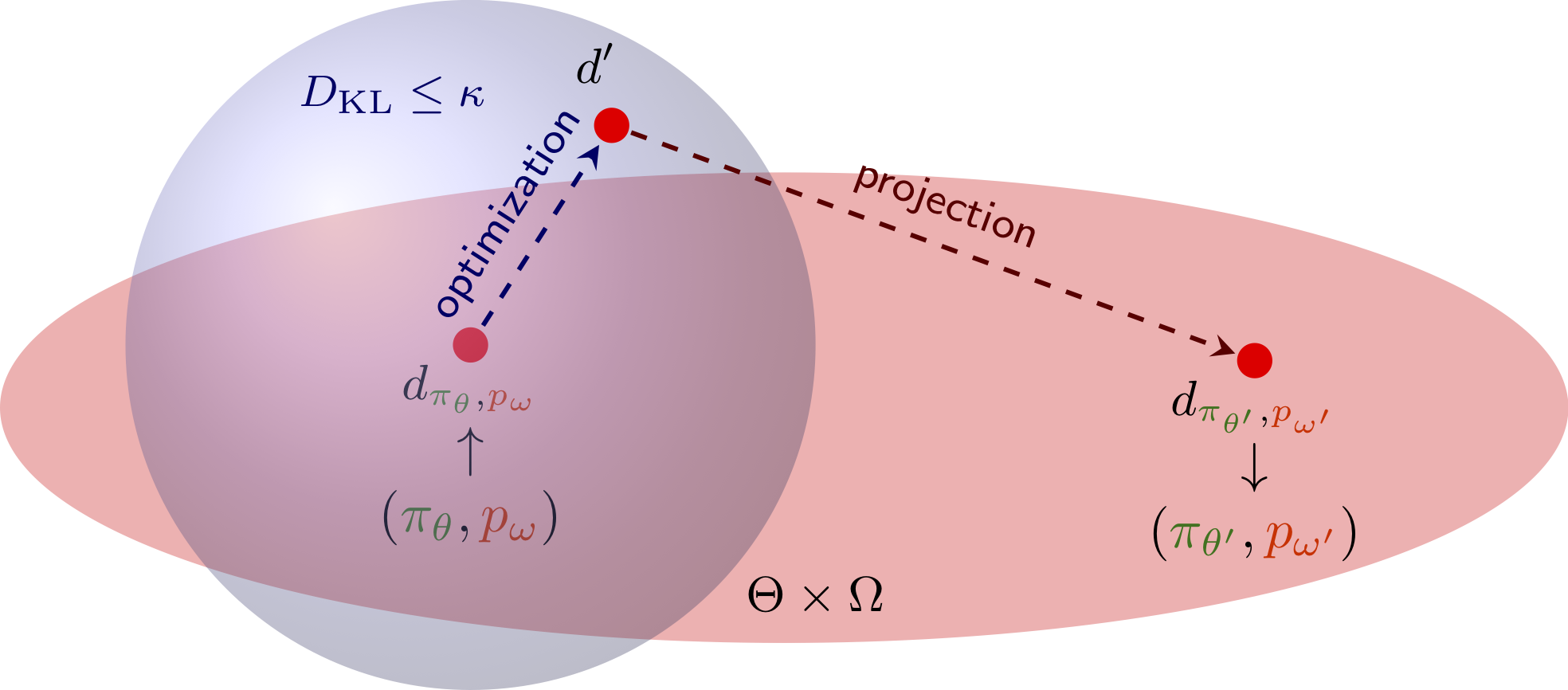
Optimization and Projection
Relative Entropy Model Policy Search (REMPS), imports several ideas from the classic REPS (Peters et al., 2010); in particular, the use of a constraint to ensure that the resulting new stationary distribution is sufficiently close to the current one. REMPS consists of two subsequent phases: optimization and projection. In the optimization phase we look for the stationary distribution that optimizes the performance. This search is limited to the space of distributions that are not too dissimilar from the current stationary distribution. The notion of dissimilarity is formalized in terms of a threshold (\( \kappa > 0 )\) on the KL-divergence. The resulting distribution may not fall within the space of the representable stationary distributions given our parametrization. Therefore, similarly to (Daniel et al., 2012), in the projection phase we need to retrieve a policy and a configuration inducing a stationary distribution as close as possible to the optimized distribution.
Model Approximation
Our formulation of REMPS requires the access to the environment dynamics \(p_\omega\), depending on the vector of configurable parameters \( \omega \). The environment dynamics represents the distribution over the next states given the current state and action: \(p: \mathcal{S} \times \mathcal{A} \rightarrow \mathcal{S}.\) In our cases the transition function depends also on some parameter: \(p: \mathcal{S} \times \mathcal{A} \times {\Omega} \rightarrow \mathcal{S}.\) Although the parameters to be configured are usually known in real word cases, the environment dynamic is usually unkown in a model-free scenario. Our approach is based on a Maximum Likelihood estimation. Given a dataset of experience: \({ ( s_i, a_i, \omega_i, s'_i )}_{i=1}^{N},\) we solve the problem:
\[\max_{\widehat{p}} \frac{1}{N} \sum_{i=1}^{N} \log \widehat{p} (s_{i}' | s_i, a_i, \omega_i).\]Once we have the model approximation \( \widehat{p} \) we can simply run REMPS replacing the true model \(p\) with the approximated model \( \widehat{p} \).
Results
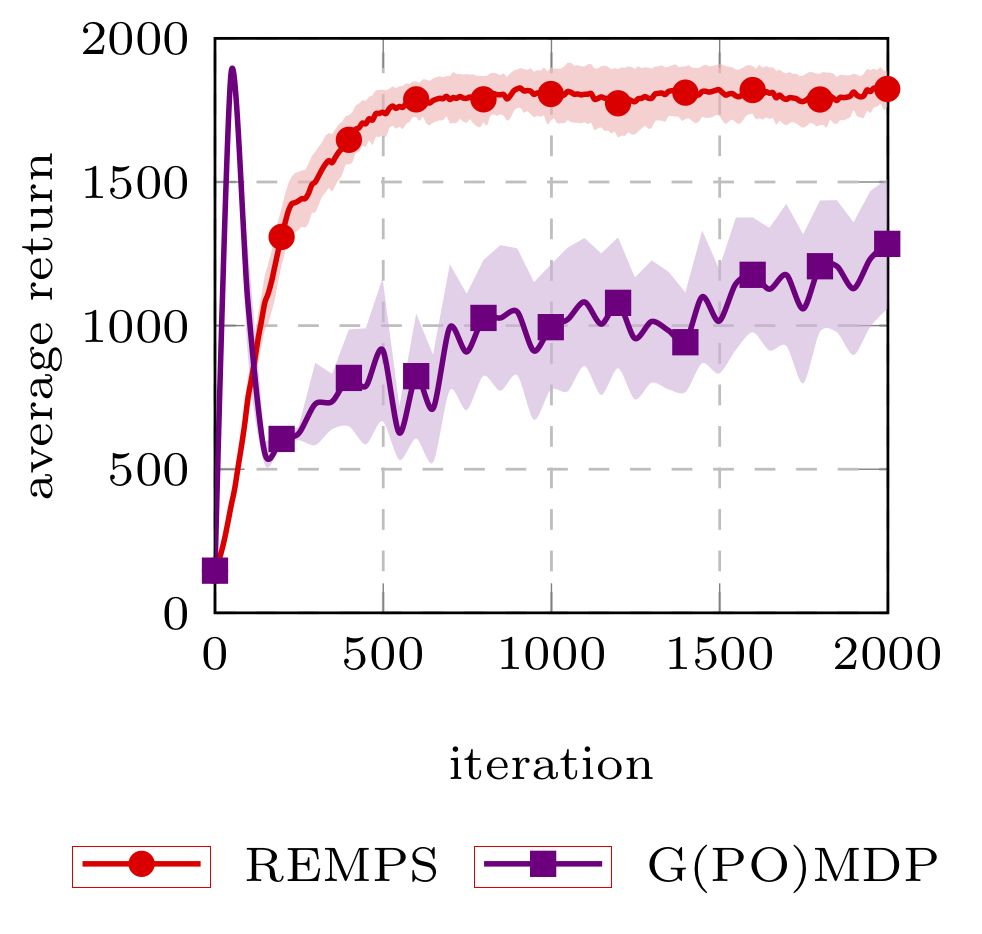
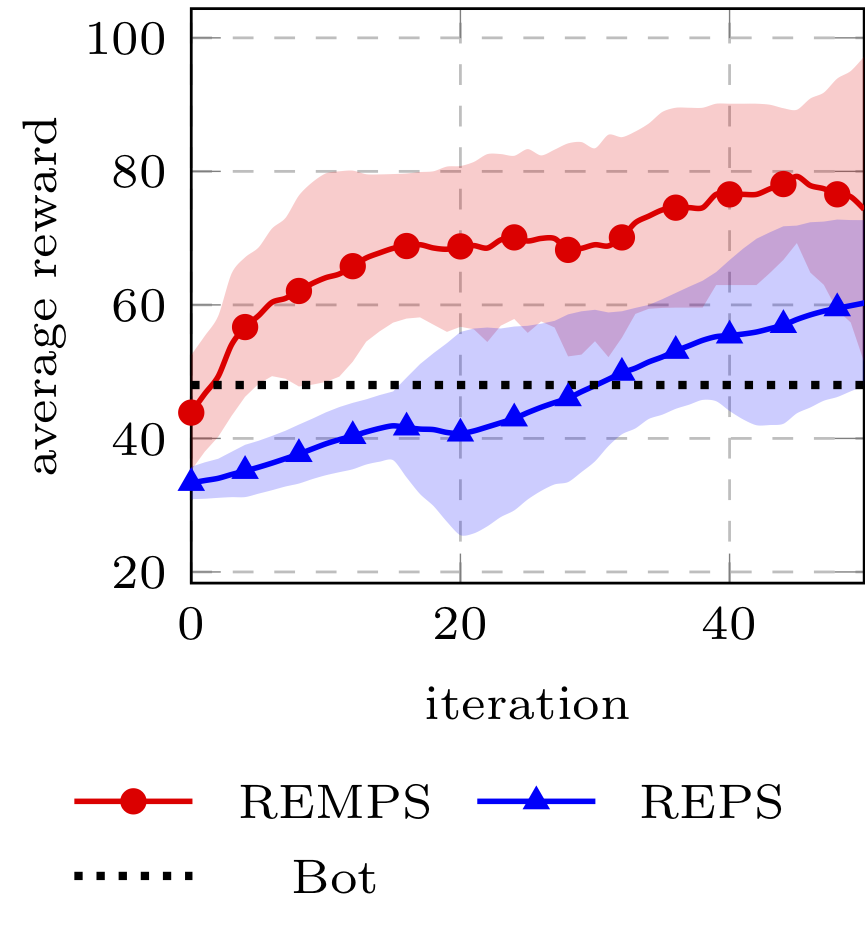
We evaluated REMPS on three domains: a simple chain domain, the classical cartpole and a more challenging car configuration task based on TORCS (Wymann et al., 2000). We compared REMPS with the extension of G(PO)MDP (Baxter & Bartlett, 2001) to the policy-configuration learning. For more details, please refer to the paper.

Authors
- Alberto Maria Metelli
- Emanuele Ghelfi
- Marcello Restelli
References
- [cmdp] Metelli, A. M., Mutti, M., & Restelli, M. (2018). Configurable Markov Decision Processes. 35th International Conference on Machine Learning, 80, 3491–3500.
- [reps] Peters, J., Mülling, K., & Altun, Y. (2010). Relative Entropy Policy Search. AAAI, 1607–1612.
- [daniel] Daniel, C., Neumann, G., & Peters, J. (2012). Hierarchical relative entropy policy search. Artificial Intelligence and Statistics, 273–281.
- [torcs] Wymann, B., Espié, E., Guionneau, C., Dimitrakakis, C., Coulom, R., & Sumner, A. (2000). Torcs, the open racing car simulator. 4, 6.
- [gpomdp] Baxter, J., & Bartlett, P. L. (2001). Infinite-horizon policy-gradient estimation. Journal of Artificial Intelligence Research, 15, 319–350.